在之前的文章中驭策原创 | 再订货点公式系列(五):服务水平,我们已经对再订货点公式主体的内容基本讲解完毕,再订货点公式背后的数学逻辑本身是非常完整与严密的,在理论层面已经很好的做到了逻辑的自洽。但是,理论还是要能够对现实产生指导作用才有其意义,而我们之前已经介绍了关于再订货点公式的各种细节,任何一个细节和实际业务对不上就有可能导致结果出现偏差,分毫不差的与公式逻辑匹配的可能性小之又小,但是不是假如不能百分之百的契合,公式就不能用了呢?其实也不然,今天我就来带着大家看看,当公式逻辑与业务逻辑不完全匹配的情况下,我们该如何使用这个公式。
01 正态分布不满足问题
对于使用再订货点公式的公司来说,首先公式的大前提,数据的正态分布估计就会难倒大部分的英雄好汉。从逻辑上来讲,由于渠道与经销商的存在,以及销售基于压货等管理诉求对需求订单的干预,最终企业收到的需求基本都很难满足正态分布。同时还要排除促销和季节性等因素的影响,所以如果想要严谨的对数据的正态分布问题进行校验,数据清洗则是必须的,清洗的方式可以参考需求计划在进行基准预测工作时的数据清洗方式。
但假设数据清洗工作已经完成,但数据依旧无法满足正态分布的情况应该怎么办呢?接下来我们就来探讨一下对于不满足正态分布的数据,我们应该如何进行处理。
首先,我们要明确一个概念,就是一组数据不论他是啥样的,我们都可以对其进行测量,并计算出这一组数据的均值与标准差,并且根据这个均值与标准差去生成对应的正态分布图形。然后将两者进行对比,在正常的业务场景中,通常会出现下列两种情况:
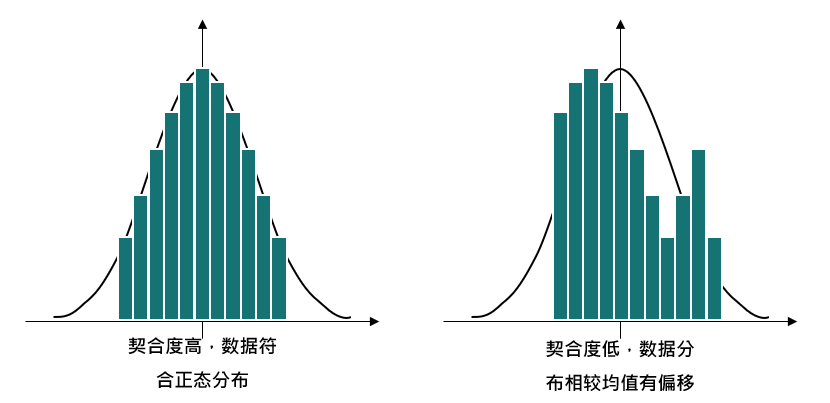
简单来说,就是一种符合正态分布,而另一种则不符合正态分布,但即使不符合正态分布,我们依旧可以与正态分布曲线进行对比。
首先我们回忆一下我们是如何利用正态分布的性质的。还是以95%对应的1.65为例,库存系数为1.65的业务含义为,假设有一百次需求,其中有95次的需求会落在1.65倍标准差的左边,即下图:
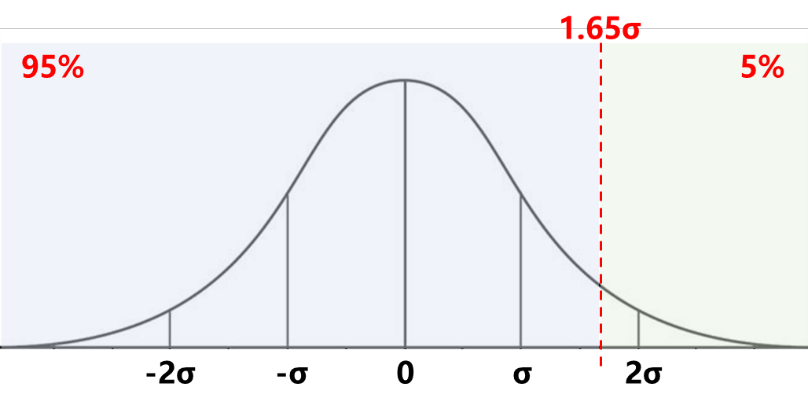
所以我们才会说服务水平有95%,这其中的关键是需求发生的次数,而假设我们的数据不符合正态分布,这里给大家提供一种量化的纠偏思路。还是以1.65倍标准差为例,计算这一组数据中,有多少个数据小于等于这组数据的1.65倍标准差。假设还是100个数据,然后我们发现有97个数据小于1.65倍标准差,那我们就可以暂定1.65的库存系数可以带来97%的服务水平。反之如果我们的目的是寻找如果我想要95%的服务水平,我该设多少的库存系数时,就可以将数据排序后,看看第95个数字等于几倍标准差,将这个倍数作为我们的库存系数即可。
但需要注意的是,由于已经脱离了再订货点公式本身的逻辑框架,所以以上方式计算出的库存系数通常只作为参考,其严谨性与逻辑性均有较大下降,最大的作用如果用大白话来讲的话就是:有参考总比没有好。
02 服务水平计算问题
第二个问题则是关于服务水平的计算问题,上一次我们说到,再订货点公式中的服务水平是按日需求是否得到完整满足来进行计算的,无法与我们通常所使用的服务水平计算方式匹配。而之所以要用到日需求,是因为只有这样才能将其与提前期L关联起来,而订单行是无法与提前期L进行关联的。在这里我要给大家道个歉,因为他们其实是可以关联的,而且答案其实再订货点公式本身已经给出来了!
再订货点公式:
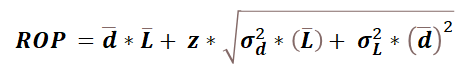
我们再来看看我们的再订货点公式,一般来说,在使用再订货点公式时,我们的注意力通常都会集中在需求的波动这一部分,因为这一部分的波动通常最为明显,而供应的波动通常会被忽视。认真学习的小伙伴应该还记得我们之前所讲,提前期在公式中其实表达的并不是一个严格的时间概念,而是在一个补货周期中需求发生的次数。那么大家注意了,关键的地方要来了,我们之前说的供应的波动,其实也就是次数的波动!我们的生产时间是相对固定的,但是每一个生产时间中产生的订单以及订单行的数量则是波动的,所以我们就可以通过对产生的订单或者订单行的数量的波动进行测算,从而替换掉公式中的“供应的波动”。通过这样的方式,就可以直接将公式中的服务水平与订单或者订单行的服务水平计算方式进行直接对接!从而将公式与实际更好的结合起来。
但需要注意的是,基于订单行数量的服务水平算法是则是无法与公式直接对接的,我们可以在换算为订单行的服务水平后再进行一个正向的修正,因为按订单行数量算出的服务水平总是高于按订单行算出的服务水平的。所以最终的服务水平相对于我们设置的库存系数对应的服务水平总归是要高的。
03 总结
除了上述的两种结构性的问题之外,我们在实际的应用中还会遇到很多其他问题。例如最典型的数据取数问题,很多公司的数据质量令人堪忧,存在大量管理与操作上的陋习,导致记录下的数据失真严重。其他的还有例如多级库存的库存设置问题,多级库存在设置库存水平时,通常是补货管理与策略占到了一半以上的作用,而再订货点公式的使用与计算只是起到一个补充的作用。以上相关问题,难以穷尽,所以在这里只能点到为止了。
再订货点公式系列写到这里已经是第六篇了,由于该系列文章涉及了大量的公式与数学知识,坚持看到这里的读者可能不多,感谢你们一路上的陪伴。之所以要写这么细,最根本的目的也就是希望大家在无法完全拿公式往业务上套的时候,能够自行的对公式进行调整与修正,或者至少能够做到方向性的偏差预估,这样我们在运用这些公式的时候,心中也会更加的有底气。
下一篇的文章应该就是我们的再订货点公式系列的最后一篇了,我将给大家展示一种全新的库存设置可能性,甚至可能会推翻我之前的这六篇文章的全部内容,库存水平计算这条路的尽头是什么?在下一篇文章中,我将从另一个角度提出一个新的进行库存设置的思路,颠覆所有试图进行库存水平计算的逻辑,大家敬请期待!

